Home
 

4. Queueing Networks with loss and blocking-1

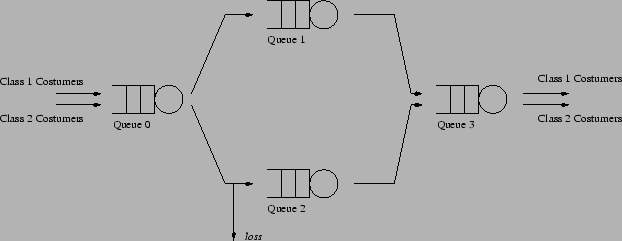
The  example refers to an open queueing network model with finite capacity queues (with blocking and loss patterns), different classes of customers, priority and complex load dependent service rates. We shall use a four-queue system with two classes of customer as indicated in figure.

Figure :Queueing network example with four queues and two classes of customer - QN model

We assume that both classes of customer enter the first service center (queue 0) with rates $\lambda_1$ for class 1 and $\lambda_2$ for class 2. Let the capacity of queue 0 be $K_0$ for customers of both classes. Once served at this center, customers of classes 1 and 2 go, respectively, to service centers 1 and 2. If queue 1 is full (its capacity is denoted by $K_1$), customers of class 1 will be blocked in service center 0. On the other hand, class 2 customers exit the system if queue 2 is full. The capacity of queue 2 is denoted by $K_2$.

In service center 0, customers of class 1 are served with a variable rate that is inversely proportional to the number of class 1 customers present in service center 3. Similarly, in this same service center, class 2 customers are served with a variable rate that is inversely proportional to the number of class 2 customers in service center 2. There is no priority between customers of classes 1 and 2 in this first service center.

In service center 1, which serves class 1 customers only, the service rate is given by $\mu_{11}$. After service here, customers enter the final service center (queue 3) if there is an available slot in the queue. Otherwise the customer is blocked. In service center 2, which serves class 2 customers only, the service rate is given by $\mu_{22}$ and again, exiting customers attempt to enter the final service center, but may be blocked.

Service center 3 provides service to both classes of customer giving priority to class 1 over class 2. Class 2 customers are served only if there are no customers of class 1 in the queue. The service rates in the service center are given by $\mu_{31}$ and $\mu_{32}$ respectively and its capacity is denoted by $K_3$.