Home
Next: 5. Model
Queueing Networks with loss and blocking
Previous: 4. Queueing network model with loss and blocking-1
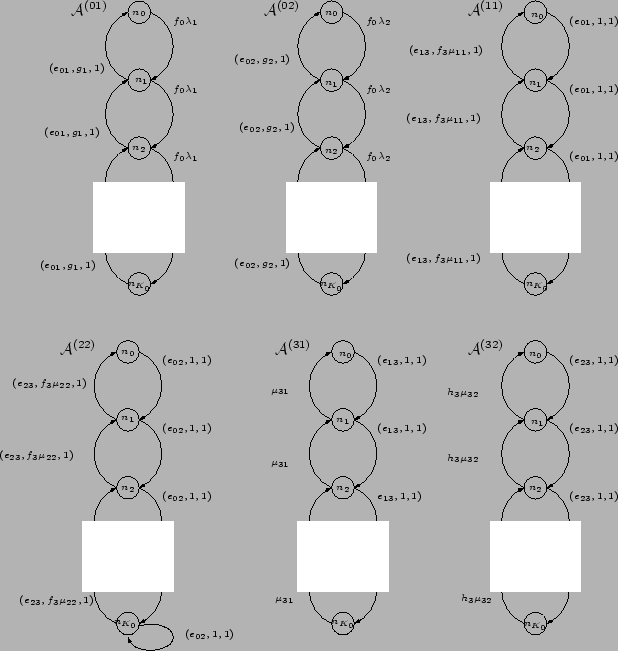
A SAN model equivalent to the queueing network model just presented
may be defined with 6 automata and functional transition rates. Two
automata are needed to describe each of the service centers visited by
both classes of customer and one automaton to describes each of the
service centers visited by only one class of customer. This SAN model
is represented graphically in Figure
and we shall refer to it as QN1.
Figure :Queueuing Network
Model -- QN1
|
Arrivals to and departures from the system are represented by
local events since they affect only one automaton. The routing of
customers between service centers occasions synchronized events since
the state of two automata are altered simultaneously. We denote such
events by  representing the departure of a
customer from service center
representing the departure of a
customer from service center  to service center
to service center  . The
event
. The
event 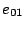 represents the departure of a class 1
customer from service center 0 to service center . The departure of
class 2 customers from service center 0 (loss behavior) is also
represented by a synchronized event even though it only changes the
state of the automaton representing class 2 customers in service center
0 (
represents the departure of a class 1
customer from service center 0 to service center . The departure of
class 2 customers from service center 0 (loss behavior) is also
represented by a synchronized event even though it only changes the
state of the automaton representing class 2 customers in service center
0 (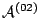 ). However since this only happens when queue 2 is full (automaton
). However since this only happens when queue 2 is full (automaton
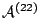 is in its last state) a synchronized
event that synchronizes the transition representing the departure of
a customer from queue 0 (an arc from state
is in its last state) a synchronized
event that synchronizes the transition representing the departure of
a customer from queue 0 (an arc from state 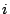 to state
to state 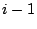 in automaton
in automaton 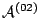 ) with the ``circular'' transition of the
last state of automaton
) with the ``circular'' transition of the
last state of automaton 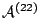 .
.
Functional rates are used to represent:
- the capacity restriction of queues represented by automata 0 and
3
- the dependent service rates in service center 0
The function 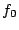 represents the capacity restriction in
queue 0. It is evaluated as true (1) if there is room for another
customer in queue 0, i.e., if the number of class 1 plus class 2
customers is less than the capacity of the queue. Hence both rates
represents the capacity restriction in
queue 0. It is evaluated as true (1) if there is room for another
customer in queue 0, i.e., if the number of class 1 plus class 2
customers is less than the capacity of the queue. Hence both rates 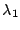 and
and 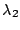 must be multiplied by
must be multiplied by 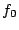 where
where
Analogously, function 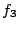 represents the capacity
restriction in queue 3, and the transition rates (
represents the capacity
restriction in queue 3, and the transition rates (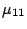 and
and 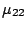 ) of the synchronized events
) of the synchronized events 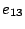 and
and 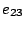 in automata
in automata
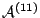 and
and 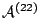 respectively must be multiplied by the
function
respectively must be multiplied by the
function
The dependent service rates in service center 0 are represented by two
functions called respectively 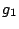 and
and 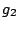 . The function
. The function 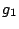 is inversely proportional to
the number of class 1 customers in service center 1 (the state of
automaton
is inversely proportional to
the number of class 1 customers in service center 1 (the state of
automaton 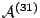 ), i.e.:
), i.e.:
The service rate of class 2 customers is analogously represented by:
The last function in this model represents the priority of class 1 over
class 2 customers in service center 3. This function must be
multiplied by the rate 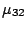 :
:
The product state space of this model is given by
However, only some of these states are reachable since obviously, the
sum of the states of automata representing the same service center
cannot be greater than the capacity of the service center.
The textual .san files
describing this model are:
Next: 5. Model
Queueing Networks with loss and blocking
Previous: 4. Queueing
network model with loss and blocking-1
Home

![]() representing the departure of a
customer from service center
representing the departure of a
customer from service center ![]() to service center
to service center ![]() . The
event
. The
event ![]() represents the departure of a class 1
customer from service center 0 to service center . The departure of
class 2 customers from service center 0 (loss behavior) is also
represented by a synchronized event even though it only changes the
state of the automaton representing class 2 customers in service center
0 (
represents the departure of a class 1
customer from service center 0 to service center . The departure of
class 2 customers from service center 0 (loss behavior) is also
represented by a synchronized event even though it only changes the
state of the automaton representing class 2 customers in service center
0 (![]() ). However since this only happens when queue 2 is full (automaton
). However since this only happens when queue 2 is full (automaton
![]() is in its last state) a synchronized
event that synchronizes the transition representing the departure of
a customer from queue 0 (an arc from state
is in its last state) a synchronized
event that synchronizes the transition representing the departure of
a customer from queue 0 (an arc from state ![]() to state
to state ![]() in automaton
in automaton ![]() ) with the ``circular'' transition of the
last state of automaton
) with the ``circular'' transition of the
last state of automaton ![]() .
.