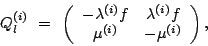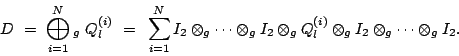Home
Next: 1.2 The same model
without functionnal rates
Previous: 1. A
Model of Resource Sharing
Figure: Resource Sharing
Model- Mutex1 -
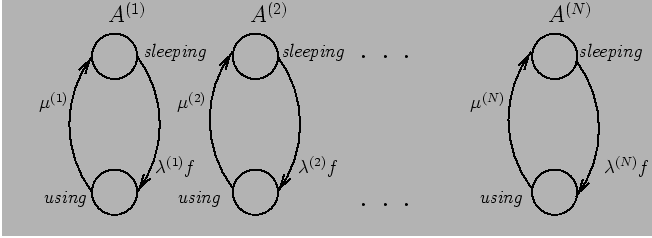 |
Each process is modelled by a two state automaton 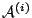 , the two states beingsleeping and using.
We shall let
, the two states beingsleeping and using.
We shall let 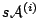 denote the current state of automaton
denote the current state of automaton 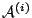 . Also, we introduce the function
. Also, we introduce the function
where 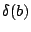 is an integer function that has the
value 1 if the boolean
is an integer function that has the
value 1 if the boolean 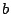 is true, and the value 0
otherwise. Thus the function
is true, and the value 0
otherwise. Thus the function 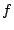 has the value 1 when access is
permitted to the resource and has the value 0 otherwise. Figure 1 provides a graphical illustration of this
model.
has the value 1 when access is
permitted to the resource and has the value 0 otherwise. Figure 1 provides a graphical illustration of this
model.
The local transition matrix for automaton 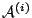 is :
is :
and the overall descriptor for the model, which does not have any
synchronizing events, is
The SAN product state space for this model is of size 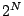 .
Notice that when
.
Notice that when 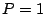 , the reachable state space is of size
, the reachable state space is of size 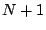 , which is considerably smaller than the product state
space, while when
, which is considerably smaller than the product state
space, while when 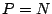 the reachable state space is the entire
product state space. Other values of
the reachable state space is the entire
product state space. Other values of 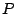 give rise to
intermediate cases.
give rise to
intermediate cases.
The textual .san files
describing this model are:
Next: 1.2 The same model without functionnal rates
Previous: 1. A Model
of Resource Sharing
Home

![]() , the two states beingsleeping and using.
We shall let
, the two states beingsleeping and using.
We shall let ![]() denote the current state of automaton
denote the current state of automaton ![]() . Also, we introduce the function
. Also, we introduce the function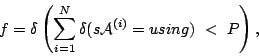
![]() is :
is :